Since I’m currently looking for a job, I try to train daily on Leetcode. I started with a now classic study plan, originally authored by Yang Shun Tay and hosted on Grind75. Eventually though, Leetcode presented me with a tiling problem that I found immediately appealing: Domino and tromino tiling.
Spoiler alert: the following content reveals the solution to the problem
If you don’t know the problem yet, take a look at the description in the link. If you are eager to solve it yourself, stop reading this post immediately. Try solving it and come back to this afterward.
I was in the process of training on bottom-up dynamic programming, and this problem lends itself perfectly to it. So let me present my conceptual solution to the problem:
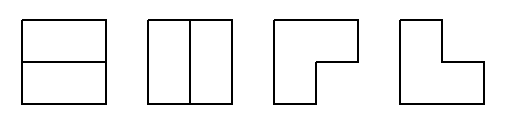
For a 2x2 (n = 2) area, only the first 2 arrangements above tile the area entirely.
But if we allow a single gap to remain on the right, either at the top or the bottom, then all 4 arrangements on the first row tile the area.
With the same rules for a 3x2 (n = 3) area, there are 9 different arrangements that (nearly) tile the area:
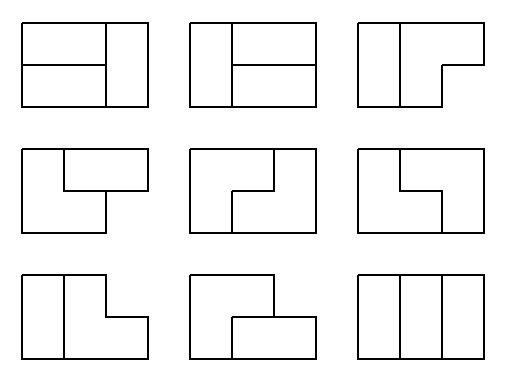
We can write the equation for the number of arrangements, according to the variables \((n, h)\), with \(h\) a boolean value representing the presence of a hole:
\begin{equation} f(n, h)= \left\{ \begin{array}{ l l } 1 & \quad \textrm{if } n = 1, h = 0 \\ 0 & \quad \textrm{if } n = 1, h = 1 \\ 2 & \quad \textrm{if } n = 2, h = 0 \\ 2 & \quad \textrm{if } n = 2, h = 1 \\ f(n - 1, 0) + f(n - 2, 0) + f(n - 1, 1) & \quad \textrm{if } n > 2, h = 0 \\ 2 f(n - 2, 0) + f(n - 1, 1) & \quad \textrm{if } n > 2, h = 1 \end{array} \right. \end{equation}
The first 4 cases should be straight-forward given the prior explanation. So let’s dig into the last 2 lines.
Imagine having to tile the \(n\)x2 area by extending it to the right from a smaller value \(n - x\). Considering only the case where there’s no hole left after, for now:
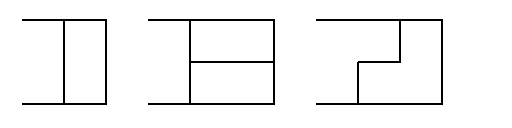
If an \(n - 1\) arrangement has no hole, placing a vertical domino to the right extends it to \(n\). If an \(n - 2\) arrangement has no hole, placing 2 horizontal dominoes to the right extends it to \(n\). Also, if an \(n - 1\) arrangement has a hole (either top or bottom), placing a single tromino to the right extends it to \(n\).
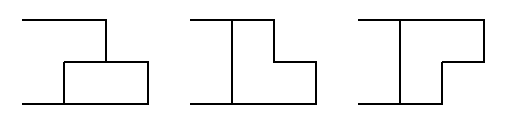
Following this same approach, in the case of a remaining hole to the right, an \(n - 1\) arrangement with a hole can be extended to \(n\) by placing a single horizontal domino and an \(n - 2\) arrangement without hole can be extended to \(n\) in 2 different ways by placing a tromino up or down.
Any other action extending \(n - x\) to \(n\) can be constructed from the 6 actions above. With this understanding, this is my initial bottom-up solution:
class Solution:
def numTilings(self, n: int) -> int:
n2h0 = 1
n2h1 = 0
n1h0 = 2
n1h1 = 2
m = 10**9 + 7
if n == 1: return n2h0
if n == 2: return n1h0
for _ in range(2, n):
n2h0, n2h1, n1h0, n1h1 = n1h0, n1h1, (n2h0 + n1h0 + n1h1) % m, (2*n2h0 + n1h1) % m
return n1h0Neat, hey?
Let’s take a look at the top answer, as one should normally do.
class Solution:
def numTilings(self, n: int) -> int:
dp=[0]*(n+1)
dp[0],dp[1]=1,1
for i in range(2,n+1):
dp[i]=2*dp[i-1]+dp[i-3]
return (dp[-1]%(10**9+7))WTF!? What is this sorcery? I spent hours arriving at my neat solution!
As one would normally find out when looking at the solutions, there’s always someone smarter than oneself. Aside from the fact that the top solution consumes more memory (due to the array and the growing integers), it does much better with a more compact equation, that does not need to consider any holes.
And, yes, there is a bit of sorcery with the negative array subscripts going on in the case \(n = 2\):
\begin{equation} f(n)= \left\{ \begin{array}{ l l } 1 & \quad \textrm{if } n = 0\\ 1 & \quad \textrm{if } n = 1\\ 2 = 2 f(1) + 0 & \quad \textrm{if } n = 2\\ 2 f(n - 1) + f(n - 3) & \quad \textrm{otherwise} \end{array} \right. \end{equation}
This equation is neat but not evident, in my opinion. Though you may have Mensa-level IQ, like this person in the comments 🫠:
Step 1: Run test cases for 1 to 8.
Step 2: Observe the relation among A[i], a[i-1] and a[i-3]Anyway, I figured my initial equation and the one above should reduce to the same form, so I was probably lazy. And indeed, when only considering cases where \(n > 2\):
\begin{equation} \begin{array}{rcl} f(n, 0) & = & f(n - 1, 0) + f(n - 2, 0) + f(n - 1, 1) & \\ \textrm{since } f(n, 1) & = & 2 f(n - 2, 0) + f(n - 1, 1) \\ f(n, 0) & = & f(n - 1, 0) + f(n - 2, 0) + 2f(n - 3, 0) + f(n - 2, 1) \\ \textrm{rearranging } f(n, 0) & = & f(n - 1, 0) + f(n - 3, 0) + \, \\ & & f(n - 2, 0) + f(n - 3, 0) + f(n - 2, 1) \\ \textrm{since } f(n - 1, 0) & = & f(n - 2, 0) + f(n - 3, 0) + f(n - 2, 1) \\ f(n, 0) & = & f(n - 1, 0) + f(n - 3, 0) + f(n - 1, 0) \\ f(n, 0) & = & 2f(n - 1, 0) + f(n - 3, 0) \end{array} \end{equation}
Damn. I hate how beautiful this is: notice how we can do away with the holes now. Here is another original explanation of the same results through a different route.
Time to rewrite the program.
class Solution:
def numTilings(self, n: int) -> int:
if n == 1: return 1
if n == 2: return 2
if n == 3: return 5
n3, n2, n1 = 1, 2, 5
for _ in range(3, n):
n3, n2, n1 = n2, n1, (2*n1 + n3) % (10**9 + 7)
return n1It happens to be similar to the 4th best solution. This should be the fastest algorithm for sufficiently large values of \(n\) though.