Programming a fast integral sine

I started playing puzzles on codingames.com recently. Although many challenges can be solved by beginners, getting to the top spots on the ladder for the toughest challenges demands a lot of time investment. Which makes it a great game.

The game I focus on is Mad Pod Racing, it plays in an arena where your bot meets another bot. Your bot has a finite amount of time for each move. This became an excuse to look into approx fast integer operations. I don’t really need to, but when I started looking at integer computations for Sine, I was swallowed whole into the rabbit hole. What could be more pointless fun than that?

I started to dig into GNU’s \(\sin x\) implementations before embarking on my journey here. The implementation is complex and is likely the product of long research. Towards the end of this article, I give a brief overview of the GNU libc IEEE754’s implementation of Sine, should you want to get into it. But that didn’t really stop me:

I’m gonna write a simple integer version of \(\sin x\) and it’s gonna be so much faster than the precise, floating point equivalent of the standard library.

Me, in a moment of pure hubris

Computing the result of such function efficiently crosses into 3 different domains: approximation, range reduction and a good understanding of what your architecture can or cannot do. Also, I was determined to waste my weekend (And most of the week — as it turned out) on this. Such an exercise is generally futile however, as the standard library implementation is already very quick.

Function Prototype

Mad Pod Racing is a hard challenge about predictions of mechanics of motion and collision. Your bot interacts with the world through standard input/output with angles expressed in degrees, using whole integers (e.g. 0, 45, 90…). Therefore, I will focus on this input domain only (whole integers expressed in degrees).

My version of \(\sin x\) is going to provide arbitrary precision, set to match the length of the hypotenuse without overflow:

int isin(int angle, int precision);

Also, I want my function to take a large input range for the degree of the angle, so I don’t need to worry about adding angles together and having to perform range reduction or modulo before using it. This is enough to meet the demands of the challenge, without compromising too much on precision. Precision is also bounded since the arena’s size for Mad Pod Racing is in the range [\(2 \cdot -10^4\), \(2 \cdot 10^4\)].

Range reduction and sine’s symmetries

Fortunately, the sine function has multiple symmetries and we don’t actually need to tackle the entire input range:

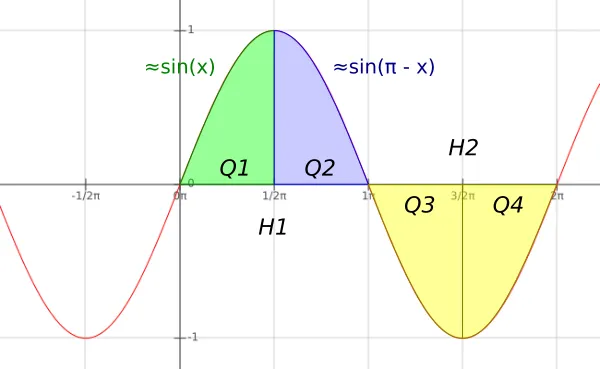
First, sine has a symmetry around x = 0. This allows us to focus on positive angles only. If the input angle was negative, we simply negate the result as well:

int isin(int angle, int precision) {
  const int slide = sizeof(int) * 8 - 1; // 31 for 32-bit int
  int s = angle >> slide;                // sign mask: 0 or -1
  int aa = (angle ^ s) - s;              // absolute angle
  // ... rest of the computation for val
  return (val ^ s) - s;                  // negate val, same as "val * s"
}

The first 3 lines need a bit of explanation. In C++, >> translates to SAR or the arithmetic bit shift to the right which carries the sign bit with it. This means that if an angle was positive then s=0x00000000, but if it was negative then s=0xFFFFFFFF or -1. This is the same principle as abs(), which I needed to decompose to keep the mask s to restore the sign to the result:

inline int abs(int a) {
  // simple abs() implementation
  int t = a >> (sizeof(int) * 8 - 1);
  return (a^t) - t;
}

Sine also has 4 quadrants, 2 halves with a period 2π; all of which are powers of 2. Thus, if we divide the input angle by a quadrant, or 90 degrees in our case, we can suddenly take advantage of the bit representation of the quotient. The symmetry between the first and second quadrant requires that we subtract the angle by 90:

int isin(int angle, int precision) {
  const int slide = sizeof(int) * 8 - 1; // 31 for 32-bit ints
  int s = angle >> slide;                // sign mask: 0 or -1
  int aa = (angle ^ s) - s;              // absolute angle
  int Qh = aa / 90;                      // quotient quadrants
  int Qr = aa % 90;                      // reminder quadrants
  int q = (Qh & 1) ? 90 - Qr : Qr;       // first quadrant symmetry
  // ... rest of the computation for val
  return (val ^ s) - s;                  // negate val, same as "val * s"
}

The last symmetry to exploit is that between the 2 halves. If we find ourselves in the top half of the trigonometric circle, the result is positive, otherwise it is negative. This is similar to the symmetry around x = 0, we just need to XOR the test for both symmetries:

int isin(int angle, int precision) {
  const int slide = sizeof(int) * 8 - 1; // 31 for 32-bit ints
  int s = angle >> slide;                // sign mask: 0 or -1
  int aa = (angle ^ s) - s;              // absolute angle
  int Qh = aa / 90;                      // quotient quadrants
  int Qr = aa % 90;                      // reminder quadrants
  int q = (Qh & 1) ? 90 - Qr : Qr;       // first quadrant symmetry
  int h = -(Qh & 2 >> 1);                // semi-circle (half) mask: 0 or -1
  // ... rest of the computation for val
  s = h^s;                               // XOR half and sign mask together
  return (val ^ s) - s;                  // negate val, same as "val * s"
}

This is the naive skeleton of our function. We only need to compute the value of sine for the reduced interval [0, 90] now.

Approximating Sine with Taylor Series

At first I decided to attempt approximation with a third order Taylor series \(T_3\) for sine:

\begin{equation} \sin x \approx T_3(x) = x - \frac{x^3}{3!} \end{equation}

This approximation is very imprecise: up to 1% error in the range [-π/4, π/4] ([-45, 45] in degrees) and errors accumulate even quicker beyond π/4. It is possible to find extra curve-fitting factors by solving a system of equations to force the point π/2 through the value 1.0: it’s already been done so I won’t go through the details. This is the resulting equation:

\begin{equation} \sin x \approx S_3(x) = \frac{4}{\pi} x - \frac{4}{\pi^3}x^3 \end{equation}

Since we are working with degrees, we can find a related solution that forces the point 90 through the value 1.0 with the same method, let’s call it \(S_{d3}\):

\begin{equation} \sin x \approx S_3(x) = ax - bx^3 \end{equation}

\begin{equation} \begin{array}{ll} S(90) &= 1 = 90 a - b90^3\\ S\prime(90) &= 0 = a - 3b90^2\\ \end{array}\rightarrow\begin{array}{ll} a &= \frac{3}{2 \cdot 90}\\ b &= \frac{1}{2 \cdot 90^3}\\ \end{array}\\ \end{equation}

\begin{equation} S_{d3}(x) = \frac{3}{2 \cdot 90}x - \frac{1}{2 \cdot 90^3}x^3 \end{equation}

To avoid sacrificing readability, I kept the form as is. This curve seems to fit sine closely when eyeballing it:

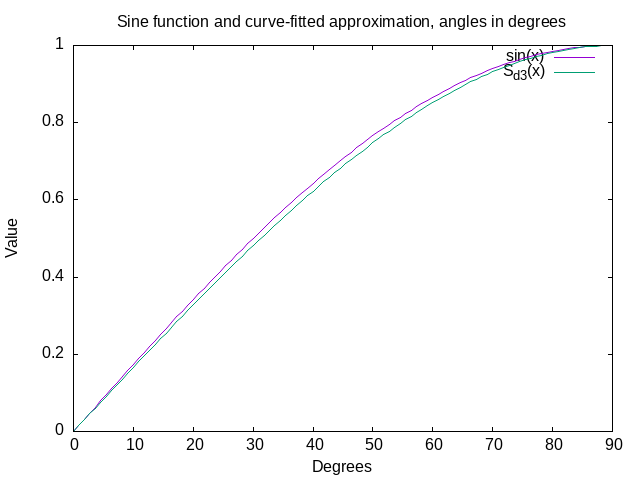
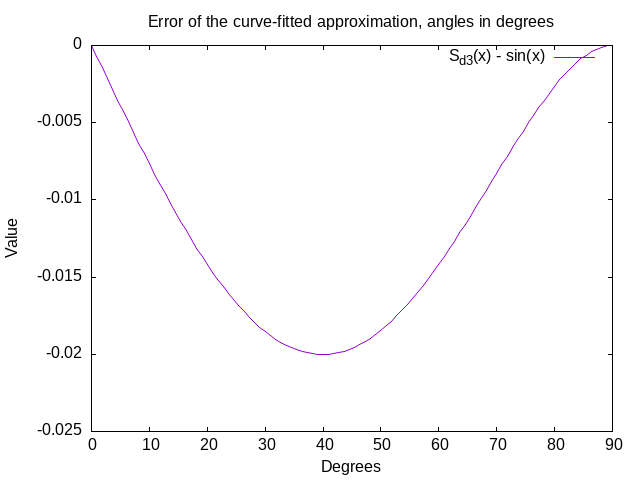
However, even this approximation is still imprecise across the range [-90, 90]. Near the 40 (or -40) degree value for the angle, the chosen approximation’s error is at its maximum (≈ 2%).

On top of that, we need to deal with overflows (and avoid underflow) in the calculation when factoring the scale. The naive implementation limits the actual range of inputs for the precision; in fact it overflows as soon as scale \(>2^{10}\), which does not cover the entire desired input domain. So we will compute the solution in the int64_t domain. We can also rearrange the operations, to minimize the numbers of divisions. This time, with the scale (or hypotenuse) H:

\begin{equation} S_{d3}(x, H) = H (\frac{3}{2 \cdot 90}x - \frac{1}{2 \cdot 90^3}x^3) \end{equation}

\begin{equation} S_{d3}(x, H) = H \frac{1}{2 \cdot 90^3} x (3 \cdot 90^2 - x^2) \end{equation}

Now there is no issues with underflow or overflow, and no compromise on precision in the entire range of scale:

inline int isin(int angle, int scale) {
  const int slide = sizeof(int) * 8 - 1; // 31 for 32-bit ints
  int s = angle >> slide;                // sign mask: 0 or -1
  int aa = (angle ^ s) - s;              // absolute angle
  int Qh = aa / 90;                      // quotient quadrants
  int Qr = aa % 90;                      // reminder quadrants
  int q = (Qh & 1) ? 90 - Qr : Qr;       // first quadrant symmetry
  int h = -((Qh & 2) >> 1);              // semi-circle (half) mask: 0 or -1
  int64_t a = (q * scale);
  int64_t b = (3 * 90 * 90 - q * q);
  int64_t c = a * b / (2 * 90 * 90 * 90);
  int val = c;
  s = h ^ s;            // XOR half and sign mask together
  return (val ^ s) - s; // negate val, same as "val * s"
}

There is still the residual error of the approximation itself. My naive implementation is also easily outclassed by implementations that consider power of 2 units for the circle instead of sticking with degrees or radians. I might re-write the above in the future, however the cost on precision should still be significant. Simply put, there’s no free lunch: we can’t have both precision and speed. Or can we?

Why not lookup everything?

Given how small the integer range is across the period (we’re talking only 180 values for the semi-circle afterall), could I not pre-compute everything? I could fix the precision since the input for the hypotenuse is bounded in the range [\(2 \cdot -10^4\), \(2 \cdot 10^4\)]. Fixing the precision to \(2^{16}\) allows me to do simple bit-shifting, after the multiplication by the hypotenuse.

constexpr const double sin_lut[180] = {
    0,                   // 0
    0.01745240643728351, // 1
    0.03489949670250097, // 2
    // ...
    0.06975647374412552, // 176
    0.05233595624294381, // 177
    0.0348994967025007,  // 178
    0.01745240643728344, // 179
};

The first step consists in creating a table of pre-computed sine values for each input degree. This table is not our final lookup table, but helps with the computation of the actual lookup table (LUT), which has the fixed precision, SinTable180points<P>.values:

template <int P> struct SinTable180points {
  constexpr SinTable180points() : values() {
    for (auto i = 0; i < 180; ++i) {
      values[i] = sin_lut[i] * P;
    }
  }
  int values[180];
};

Thanks to C++’s constexpr, we can ensure all this is done at compilation time. The new sin_lut() fixed precision function removes the need for any calculations and is as precise as needed for the entire scale of the domain (and we can easily extend it):

inline int isin_lut(int angle) {
  // Static table with precalculated outputs
  static constexpr const auto table = SinTable180points<2 << 15>();
  const int slide = sizeof(int) * 8 - 1; // 31 for 32-bit int
  int s = angle >> slide;                // sign mask: 0 or -1
  int aa = (angle ^ s) - s;              // absolute angle
  int h = aa / 180;                      // quotient semi-circle
  int ha = aa % 180;                     // reminder semi-circle
  h = -(h & 1);                          // semi-circle mask: 0 or -1
  s = h ^ s;                             // XOR semi-circle and sign together
  return (table.values[ha] ^ s) - s;
}

Was it worth it?

When micro-benchmarking all 3 approaches std::sin, isin and isin_lut, I get the following results on my machine, which should be easily reproducible. All benchmarking is done after warm-up by computing over 1440 fixed points multiple times and averaging the results:

The tests attempts to make the compare each function as closely as possible by using the same precision when possible. However we should realise 2 things: std::sin() and sin_lut() do not compromise on precision, only isin() does. It’s quite remarkable, therefore, that the lookup table version is so quick and yet uncompromising. Nevertheless, I was impressed by how fast std::sin() is.

This entire exercise was personally educational but ultimately unnecessary for the needs of the challenge. The standard library implementation is already fast enough, and I have a better appreciation for it now. There is evidently much more I can squeeze out of the approximation (I worked on this without much prior knowledge) and maybe I’ll return to it in a future post.

The source code for this project can be found here.

Further reading

The standard library implementation of sine combines multiple techniques, some of which are already explored above: range reduction, Taylor approximation, lookup tables. It also makes uses of additional techniques which are not covered here, but it is a hard read.

While working on the approximation, I stumbled across another post that would have required much content to be rewritten, had I followed through with what I learned there. Notably, the approximation (S3) is nearly twice faster than isin_lut in my own tests, even if its suffer from imprecision too (still ≈2%) when having to convert from degrees. It’s a great read in any case, and it’s already linked in other places above: http://www.coranac.com/2009/07/sines/